Skip to main content

​
Tooltip Overview

A tooltip with key statistics and deeper information is shown if you hover over a metric in Pulse.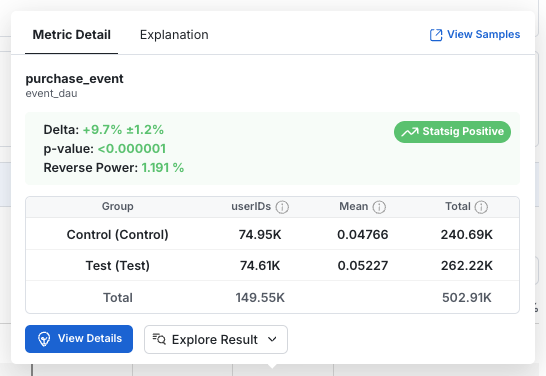
UI for metric hover card in experiments
  • Group: The name of the group of users. For Feature Gates, the “Pass” group is considered the test group while the “Fail” group is the control. In Experiments, these will be the variant names.
  • Units: The number of distinct units included in the metric. E.g.: Distinct users for user_id experiments, devices for stable_id experiments, etc.
  • Mean: The average per-unit value of the metric for each group.
  • Total: The total metric value across all units in the group, over the time period of the analysis.

​
Calculation details

Metric TypeTotal CalculationMeanUnits
event_countSum of events (99.9% winsorization)Average events per user (99.9% winsorization)All users
event_userSum of event DAU (distinct user-day pairs)Average event_dau value per user per day. Note that we call this “Event Participation Rate” as this can be interpreted as the probability a user is DAU for that event.All users
ratioOverall ratio: sum(numerator values)/sum(denominator values)Overall ratioParticipating users
sumTotal sum of values (99.9% winsorization)Average value per user (99.9% winsorization)All users
meanOverall mean valueOverall mean valueParticipating users
user: dausum of daily active usersAverage metric value per user per day. The probability that a user is DAUAll users
user: wau, mau_28dayNot shownAverage metric value per user per day. The probability that a user is xAUAll users
user: new_dau, new_wau, new_mau_28dayCount of distinct users that are new xAU at some point in the experimentFraction of users that are new xAUAll users
user: retention metricsOverall average retention rateOverall average retention rateParticipating users
user: L7, L14, L28Not shownAverage L-ness value per user per dayAll users

​
p-Value

In Null Hypothesis Significance Tests, the p-value is the probability that such an extreme difference can arise by random chance when the experiment or test actually has no effect. A low p-value implies the observed difference is unlikely due to random chance. In hypothesis testing, a p-value threshold is used to determine which results are due to a real effect and which are plausibly due to random chance. (p-value calculation)

​
Reverse Power

Reverse power is the smallest effect size that an experiment can reliably detect in its current state (some studies refer to this value as ex-post MDE). It is calculated from the sample size and standard error from the control group. Importantly, reverse power does not depend on the observed effect size. In practice, reverse power answers such questions like: given how the test actually played out, what is the smallest effect we have sufficient power (typically 80%) to detect? For a two-sided test, the reverse power for a given metric X is computed using the following equation: ReversePower=(Z1−β+Z1−α/2)X‾control×var(ΔX‾)Ncontrol×100%Reverse Power = \frac{(Z_{1-\beta} + Z_{1-\alpha/2})}{\overline{X}_{\text{control}}}\times \sqrt{\frac{\mathrm{var}(\Delta \overline{X})}{N_{\text{control}}}} \times 100\% For a one-sided test, the reverse power for a given metric X is computed using the following equation: ReversePower=(Z1−β+Z1−α)X‾control×var(ΔX‾)Ncontrol×100%Reverse Power = \frac{(Z_{1-\beta} + Z_{1-\alpha})}{\overline{X}_{\text{control}}}\times \sqrt{\frac{\mathrm{var}(\Delta \overline{X})}{N_{\text{control}}}} \times 100\%
  • X‾control\overline{X}_{\text{control}} is the mean metric value across control users
  • var(ΔX‾)var(Δ\overline{X}) is the population variance of delta
  • NcontrolN_{\text{control}} are the observed number of units in the control group
  • Z1−βZ_{1-\beta} is the standard Z-score for the selected power. Typically 1−β{1-\beta} = 0.8 and Z1−βZ_{1-\beta} = 0.84
  • Z1−α/2Z_{1-\alpha/2} and Z1−αZ_{1-\alpha} are the standard Z-scores for the selected significance level in a two-sided test and in a one-sided test.
You can enable reverse power as an optional feature. To manage it, go to Settings -> Product Configuration -> Experimentation -> Organization, where you can toggle it on or off.

​
Detailed View

Click on View Details to access in depth metric information. The detailed view contains three sections:
  • Time Series: How the metrics evolve over time
  • Raw Date: Group level statistics
  • Impact: How the experiment impacts the metric

​
Time Series

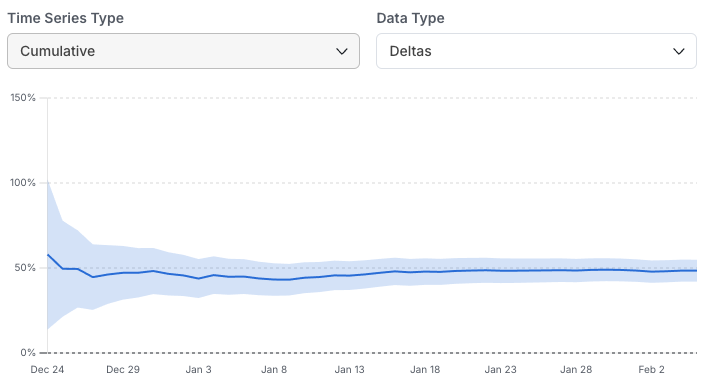
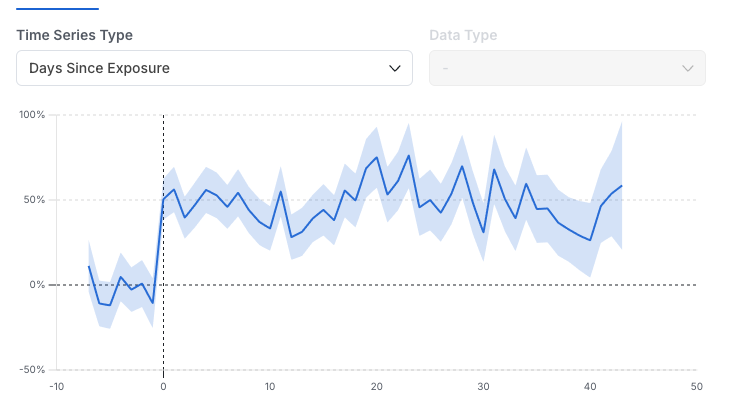
In this view, select and drag as needed to zoom-in on different time ranges. Three types of time series are available in the drop-down: Daily: The metric impact on each calendar day without aggregating days together. This is useful for assessing the variability of the metric day-over-day and the impact of specific events. It’s the recommended time series view for Holdouts, since it highlights the impact over time as new features are launched.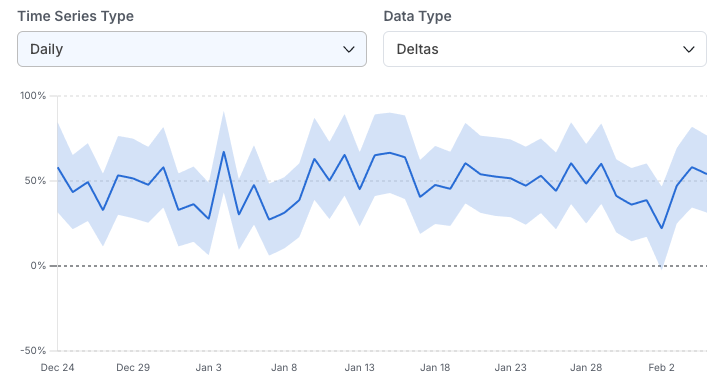
Daily metric impact visualization interface
Cumulative: Shows the cumulative metric impact from the start of experiment over time. This is a good way to observe trends and see how your confidence interval changes over time.
Cumulative metric lift visualization interface
Days Since Exposure: Shows the metric impact based on how long a user has been in the experiment. Daily data for each user is aligned by the day they entered the experiment (Day 0, Day 1, …etc), not by calendar date. This allows you to distinguish early (novelty) from long-term effects. This view also shows pre-experiment data which identifies biases between groups before the experiment started. This can happen due to random chance or by some issue in the random assignment process.
Days since exposure metric visualization interface

​
Raw Data

This view shows the group level statistics needed to compute the metric deltas and confidence interval. Includes Units, Mean, and Total (explained above), as well as the Standard Error of the mean (Std Err). Details on the statistical calculations are available here.

​
Impact

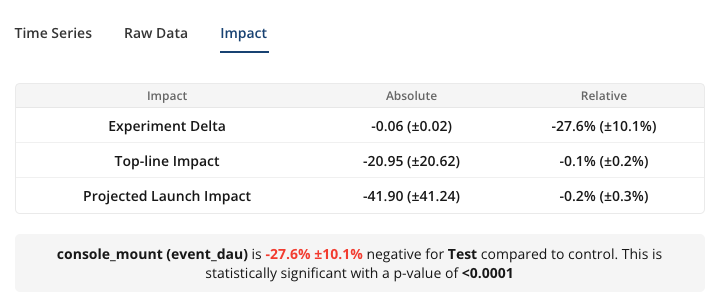
Experiment impact metrics interface
  • Experiment Delta (absolute): The absolute difference of the Mean between test groups i.e. Test Mean - Control Mean.
  • Experiment Delta (relative): Relative difference of the Mean i.e. 100% x (Test Mean – Control Mean) / Control Mean
  • Topline Impact: The measured effect that experiment is having on the overall topline metric each day, on average. Computed on a daily basis and averaged across days in the analysis window. The absolute value is the net daily increase or decrease in the metric, while the relative value is the daily percentage change.
  • Projected Launch Impact: An estimate of the daily topline impact we expect to see if a decision is made and the test group is launched to all users. This takes into account the layer allocation and the size of the test group. Assumes the targeting gate (if there is one) remains the same after launch.
See here for details on the exact calculation for topline and projected impact. FAQs about topline impact Why is the projected launch impact smaller than the relative experiment delta? Often times, an experiment can impact only a subset of the user base that contributes to a topline metric. So the relative experiment delta that we observe is effectively diluted when measured against the topline metric value. For example: Consider a top-of-funnel experiment on the registration page. Among users that hit this page, the treatment is leading to more sign ups and a 10% lift in daily active users (DAU). However, our topline DAU metric includes other user segments outside of the experiment, such as long term users that don’t go to the registration page. So what was a 10% lift in the test vs. control comparison, may amount to only a 1% increase in overall DAU. How can the topline impact be higher than the experiment delta? It’s possible for the topline impact to be higher or lower than the experiment delta. This is because the two values are computed differently and have different meaning. Experiment deltas are based on the unit-level averages: The mean value of the metric is computed for each user across all days, and then averaged to obtain the group mean. The topline impact is computed daily based on the total pooled effect from all users, and we take the average across days to show the daily impact. We chose to compute topline impacts in this way because most metrics are tracked on a daily basis and the topline value tends to be computed as an aggregation across all users, rather than a user-level average. For experiment analysis, on the other hand, best practice is for the analysis unit to match the randomization unit, so metrics are aggregated at the unit level first before computing experiment deltas.