Sequential Probability Ratio Tests

What is SPRT?

The Sequential Probability Ratio Test (SPRT) is another, advanced methodology for running AB tests, differing from the traditional Null Hypothesis Significance Test (commonly called Frequentist analysis). SPRT can meaningfully improve time to decision for your experiments, including detecting unwanted metric regressions much faster. It also tends to be much easier to share results to stakeholders who aren't super familiar with P-values and Significance levels. Lastly, SPRT has no penalties for peeking; there's no need for sequential testing plans, Alpha spending, or CI-penalties as SPRT is built to be a sequential test methodology from the start.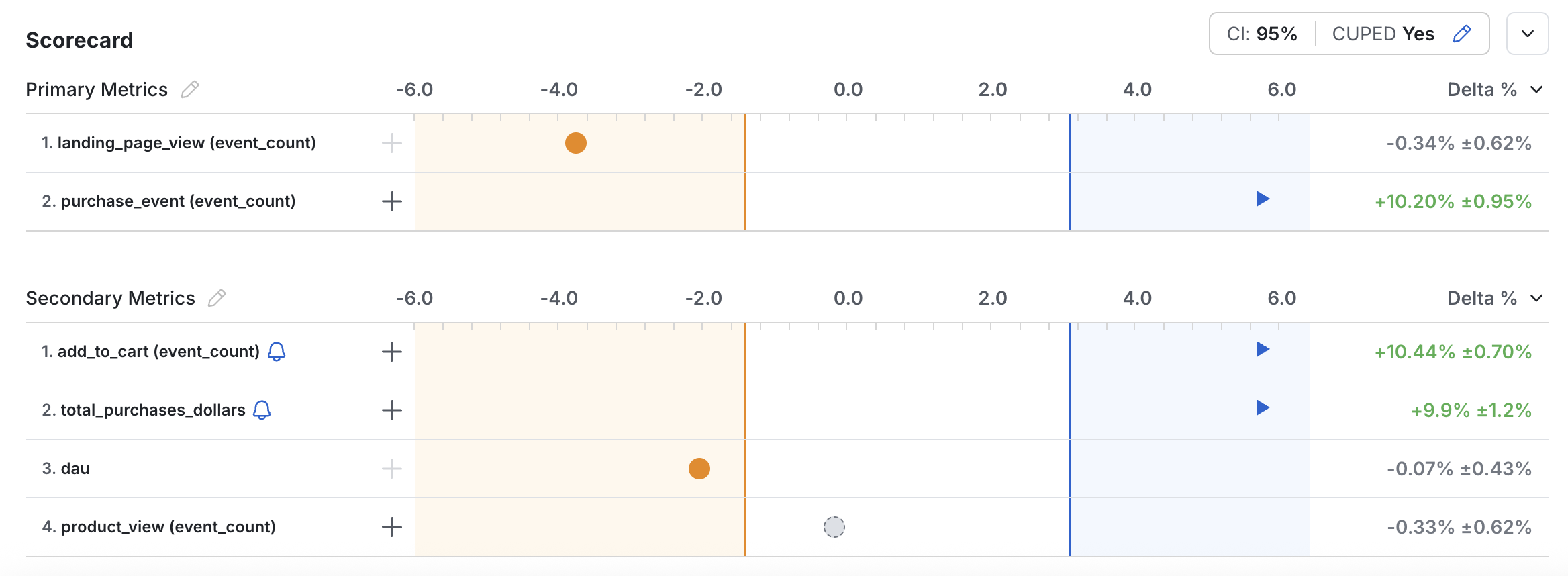

Concepts

SPRT introduces a few key concepts that differ from standard Frequentist tests. At its core, SPRT relies on the Likelihood Ratio (LR) and Upper and Lower decision boundaries, A and B.

The Likelihood Ratio estimates the relative difference in the likelihood of two outcomes:

• Numerator: What you observe is due to an alternative hypothesis (you set) being correct.
• Denominator: What you observe is due to the null hypothesis being correct.

The Upper and Lower decision boundaries are determined by your joint tolerances for Type I and Type II errors.

• A: If LR exceeds this upper threshold, you should accept the Alternative Hypothesis.
• B: If LR is less than this lower threshold, you should accept the Null Hypothesis.
• When LR falls into the range between these thresholds, no decision can be made and you should continue collecting data.

An LR of 5.8, for example, indicates that the what you observed is 5.8x more likely under the alternative hypothesis as compared to the null hypothesis.

One of the nice things about SPRT is that this Likelihood Ratio is similar to how most people think about comparing options. Rather than reporting P-values and Significance levels, you can now report a result like "With an LR of 3.5, it's 3.5x more likely that the feature worked."

Why SPRT?

• Faster Decisions: SPRT allows you to reach conclusions more quickly, potentially reducing experiment run time.
• Intuitive Results: Instead of p-values, SPRT uses the Likelihood Ratio, a more intuitive measure of evidence for or against your hypotheses.
• Sequential Analysis: Data is continuously evaluated as it is collected, allowing for early stopping when sufficient evidence is reached. There's no penalty for "peeking" in SPRT experiments.
• Clear Outcomes: SPRT enables you to confidently accept either the Null or Alternative hypothesis, rather than just “rejecting the null.”
• Data-Informed: Statsig’s implementation uses your past data and power analysis to inform the likelihood calculations and decision thresholds.

Comparing SPRT to other analysis methods

Category	Frequentist	SPRT
Test Statistic	P-value	Likelihood Ratio
Decision Threshold	Alpha	A & B
Decision Framework	Reject/Fail to Reject the Null	Accept the Null, Accept the Alternative Hypothesis, Or Continue
Allows Peeking	Yes, but with Sequential Testing Penalties	Yes, Unlimited
Requires Pre-Setup	No, but highly recommended	Yes, per metric
Allows 1- and 2-Sided tests	Yes, per metric	Yes, per metric

How to Use SPRT in Statsig

Enabling SPRT: Select SPRT as your analysis method when setting up an AB test in the Statsig console.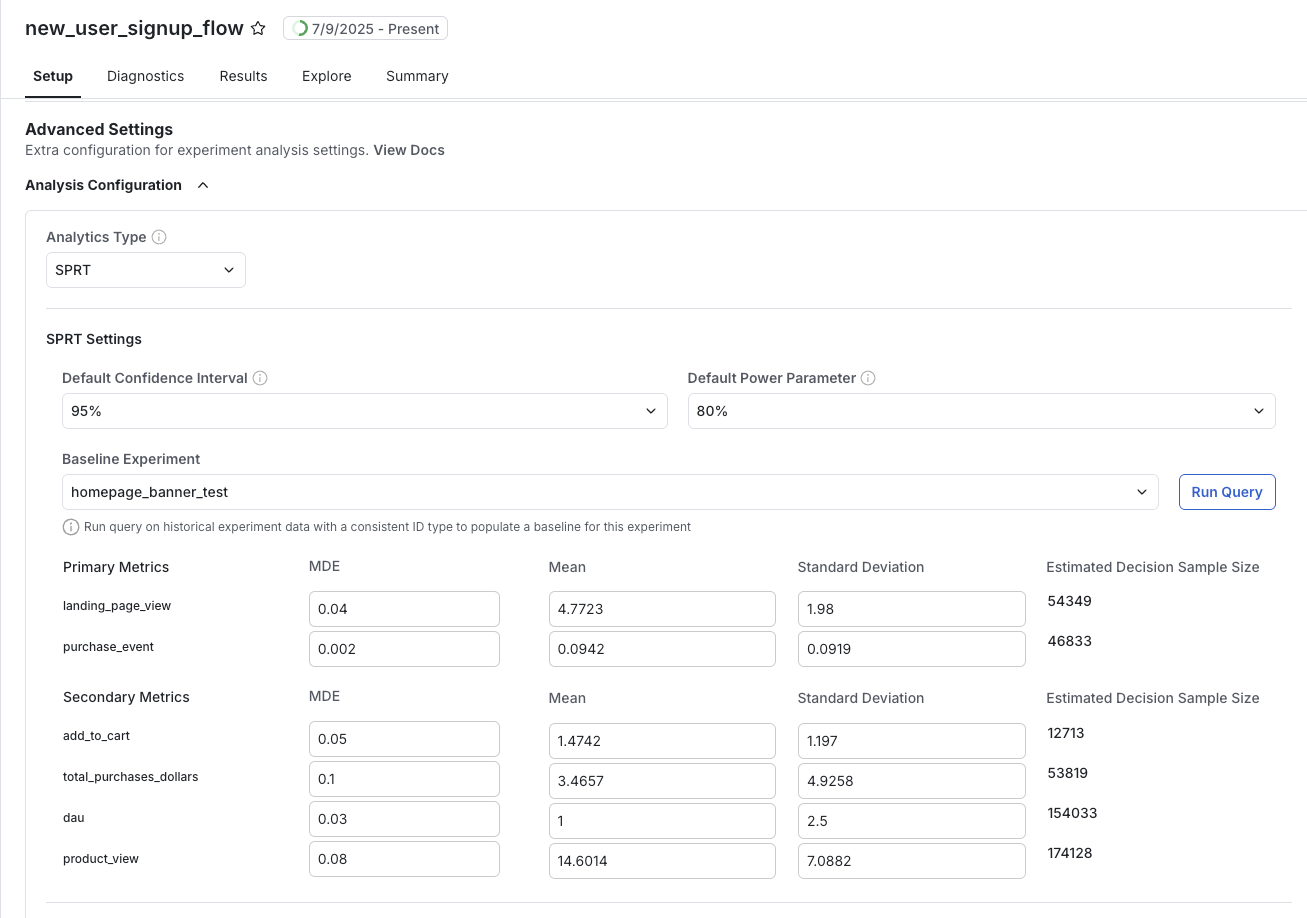

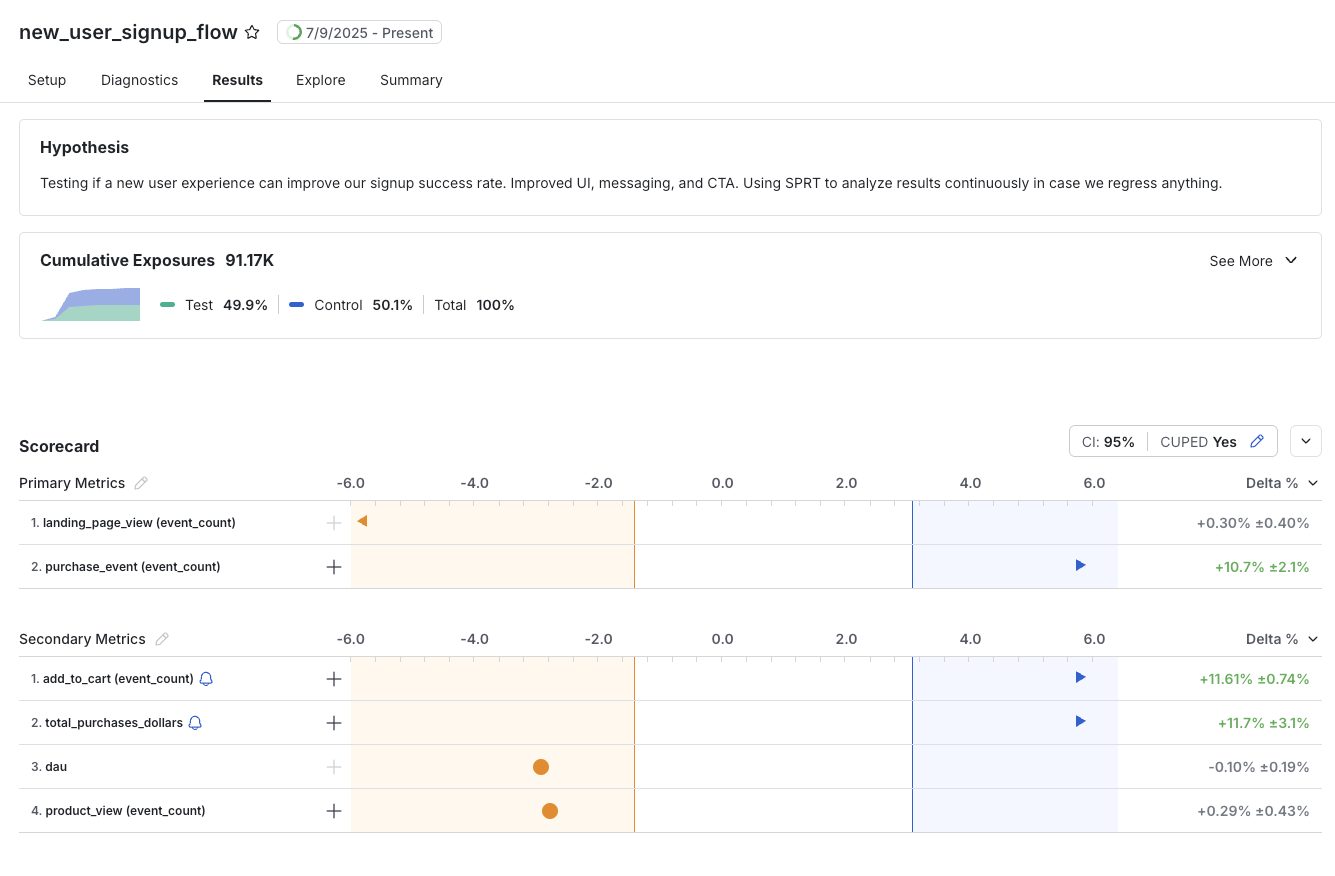
Interpreting Results: The experiment Results tab shows the latest likelihood ratio for each metric in your experiment and indicates when a decision boundary has been reached, allowing you to accept the null or alternative hypothesis with confidence.

Computing SPRT Results

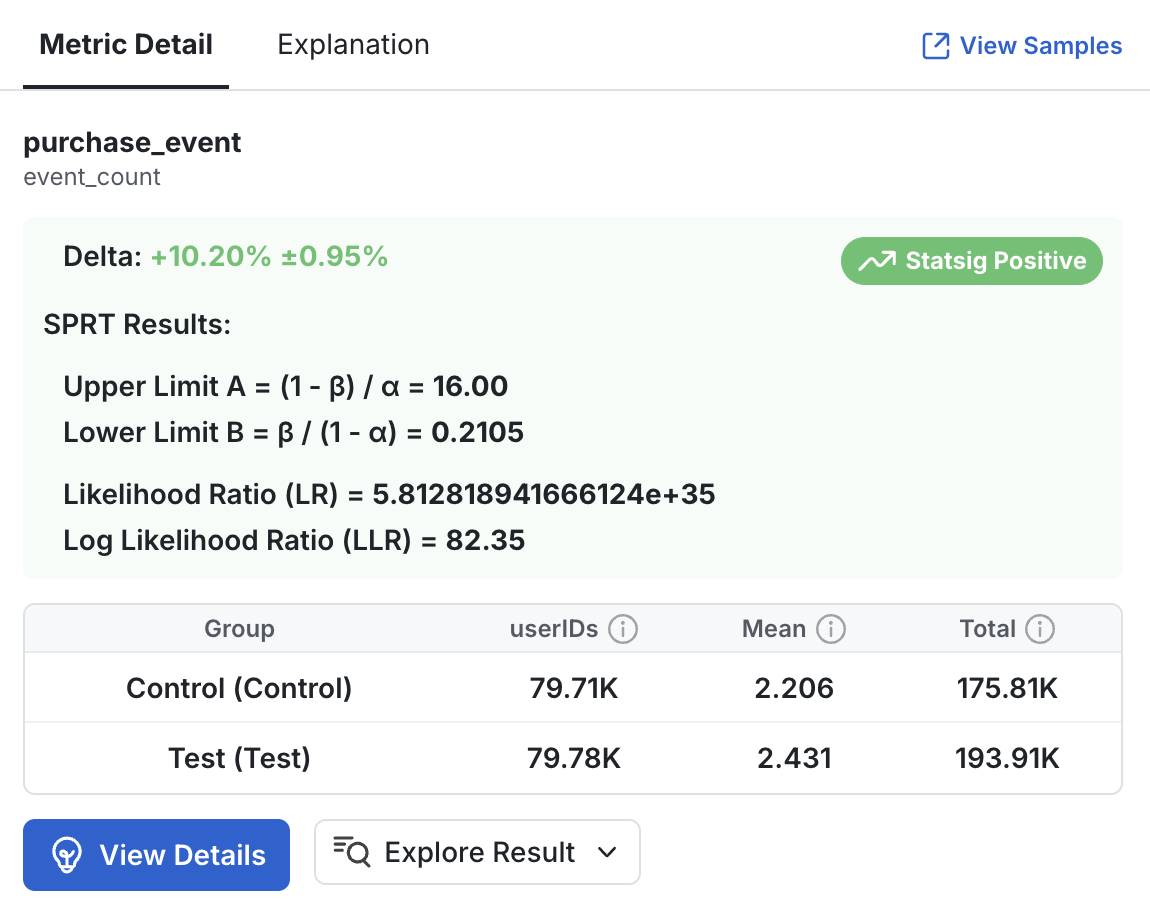
Statsig uses an updated version of Hajnal's two-sample t test, as modified by Derek Ho of Atlassian (ref TBD), in our SPRT calculations.

On each day, compute the following for a comparison between any two groups A and B for a specific metric:

$$\LARGE {LR} = \frac {\phi(|z_{m}|; \theta, 1)} {\phi(|z_{m}|; 0, 1)}$$

where:

• $\Large \phi(x; \theta, 1)$ is the PDF of a normal distribution of shape $\Large \mathcal{N}(\theta, 1)$ evaluated at $\Large x$
• $\Large z$ is the observed Z-statistic between the groups $$\Large z = \frac {\Delta \bar{X}} {\sigma_{\Delta\bar{X}}} = \frac {\bar{X}_B - \bar{X}_A} {\sigma_{\Delta\bar{X}}}$$

$$\Large \sigma_{\Delta\bar{X}}=\sqrt{\frac{var(X_A)}{N_A}+\frac{var(X_B)}{N_B}}$$

• $\Large \theta$ is derived from Cohen's d set prior to the experiment for the particular metric being considered

$$\Large \theta = \frac {\delta} {\sqrt{ \frac{1}{N_A} + \frac{1}{N_B} }}$$

• $\Large N_{A}$ and $\Large N_{B}$ are the number of observed units for each group

Power Analysis & Setting Cohen's d

SPRT requires that a value of Cohen's d be set prior to the start of the experiment for each metric being evaluated. Setting the parameter requires three components:

• MDE: An Minimum Detectable Effect desired to be measured, in units of percent
• Mean: A baseline average value for the metric, $\Large \overline{X}$
• Standard Deviation: A baseline standard deviation for the metric, $\Large \sigma_{X}$

With them, it's easy to compute Cohen's d parameter for each metric:

$$\Large \delta = \frac{\text{MDE\%} \cdot \overline{X}}{100 \cdot \sigma_{X}}$$

This process can be automated using Statsig's built-in query tooling. If you have a past experiment that ran on a similar set of units expected in the upcoming experiment, this can be configured as a Baseline Experiment and a query will automatically pull the relevant metric parameters for your metrics. Users can also input all 3 parameters by hand if desired.

Estimating the decision sample size

While Cohen's d is used to compute your experimental results after the experiment starts, it can also be used to estimate the duration of an experiment in advance. Given SPRT allows users to look at results as often as desired, this is not the same as a "required sample size" in traditional frequentist testing. The Decision Sample Size is an estimate of the number of samples that will be sufficient for SPRT result for a metric to exceed either threshold and accept one of the hypotheses.

Given:

$$\Large A=ln\left(\frac{1-\beta}{\alpha}\right)$$ $$\Large k=\frac{n_{ec}}{n_{et}}=\frac{\text{units expected in control}}{\text{units expected in treatment}}=\frac{\text{\% units expected in control}}{\text{\% units expected in treatment}}$$ $$\Large n_{et} = \frac{A}{\frac{1}{2}\left(\frac{k}{1+k}\right)\delta^2}$$

Then, the total number of expected units at decision time is:

$$\Large n_e=n_{et}+n_{ec}=n_{et}(1+k)$$

References

• Original SPRT Paper (Wald, 1945)
• The Sequential Probability Ratio t Test (Schnuerch & Erdfelder, 2020)
• A two-sample sequential t-test (Hajnal, 1961)

FAQ

Can I use SPRT for all experiments?
SPRT is best suited for experiments where you want faster, sequential decisions and are comfortable with likelihood-based inference. For some experiment types, traditional methods may still be preferable.

How does SPRT affect experiment duration?
SPRT can reduce experiment duration, especially when there is strong evidence for or against an effect. However, if the effect is small or data is noisy, the test may run longer.

What are the limitations?
SPRT requires careful setup of thresholds and assumptions. It is not a drop-in replacement for all frequentist methods, and may not be suitable for all experiment types.

Is SPRT the same as Sequential Testing? SPRT is different from our Sequential Testing option. Sequential Testing adjusts your Frequentist analysis method to allow repeated looks (i.e. "peeking"). SPRT is a completely separate experimental procedure and decision framework. They both allow for continuous "sequential" looking at experiment results, but otherwise they are separate methods for designing and running an A/B test.