Power Analysis

The power analysis tool leverages the known mean and variance of a metric and the observed traffic volume to estimate the relationship between three variables:

• Minimum detectable effect (MDE): The smallest change in the metric that the experiment can reliably detect. For example: An MDE of 1% with Power set to 80% means that if there's a true effect of 1% on our metric, we expect the experiment will have an 80% chance to produce a statistically significant result. If the magnitude of the true effect is smaller than 1%, it will be less likely to produce a statistically significant result (though it can still occur).
• Number of days or exposures: How long the experiment is active and the number of users enrolled in it. Longer running experiments typically have more observations, leading to tighter confidence intervals and smaller MDE. We use historical data to estimate the number of new users that would be eligible for the experiment each day.
• Allocation: The percentage of traffic that participates in the experiment. Larger allocation leads to smaller MDE, so it's often desirable to allocate as many users as possible to get faster or more sensitive results. When there's a risk of negative impact or a need for mutually exclusive experiments however, it's useful to know the smallest allocation that can achieve the desired MDE.

Using the Tool

It can be accessed from the tools menu. It's also available on the experiment setup page.

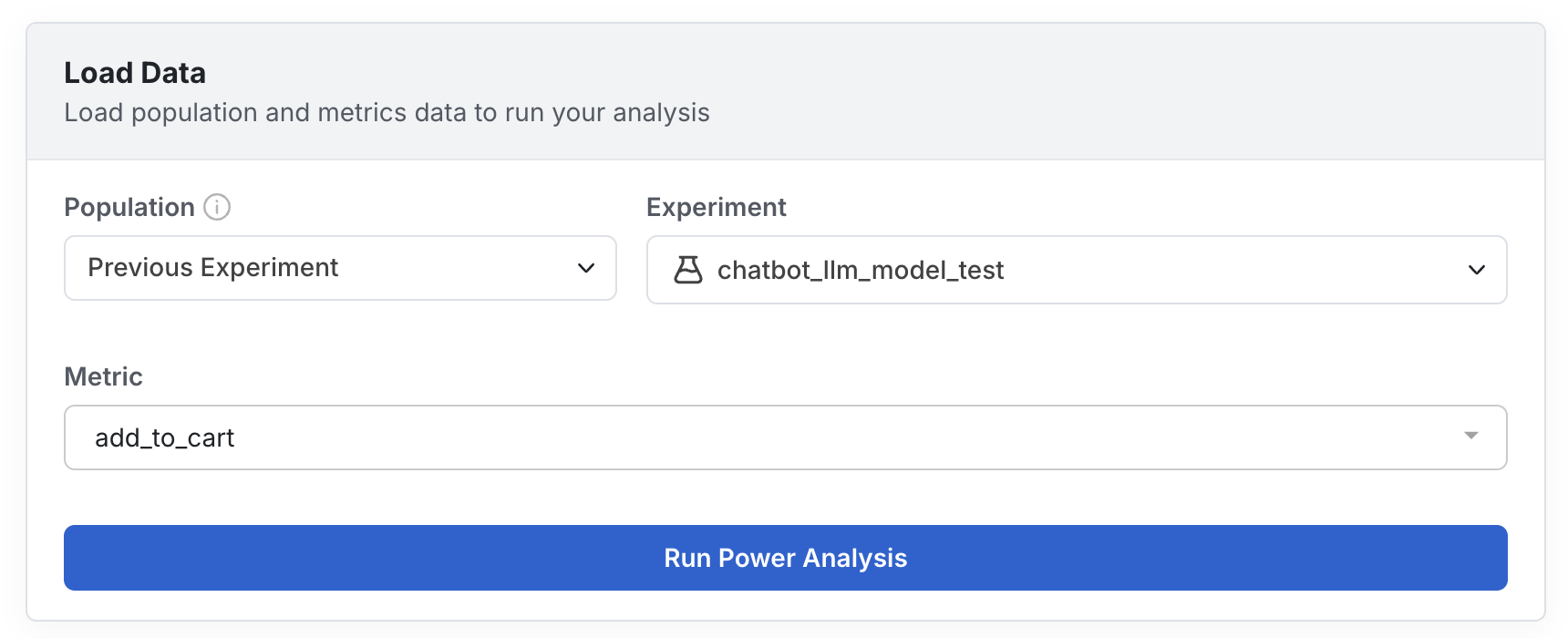
1. Select the population used to determine the metric mean and variance and to estimate the number of exposures over time.

   • Everyone: Analysis is based on the entire user base.
   • Targeting gate: Analysis is scoped to the set of users who pass the selected feature gate, which must have been active for at least 7 days. Choose this option when you plan to use a targeting gate for the experiment.
   • Past experiment: Analysis is based on data collected from in a previous experiment. Use this option when the new experiment will impact a similar user base or part of the product as the previous one.
   • Qualifying event: Analysis is scoped to the set of users who logged the event specified.

2. Select a metric of interest (or multiple metrics for a targeting gate analysis)

3. Select the type of analysis to perform:

   • Fixed Allocation: You know the available allocation, the tool tells you the expected MDE for each duration
   • Fixed MDE: You know the effect size you want to measure, the tool tells you the allocation and duration needed

4. Click on Start Calculation to see the results

   

Population Types

The population selected directly impacts the inputs of the analysis (mean, variance, number of users). To obtain reliable power analysis estimates, the metric values of the selected population should roughly match those of the users you'll be targeting in the experiment.

Example

Say we want to test a change in the checkout flow and we want to know our expected MDE for total_purchases. Let's assume that only ~10% of our daily users reach the checkout page. If we use the Everyone population for our analysis, we're likely to:

• Overestimate the number of users that the experiment will get.
• Underestimate the mean value of the total_purchases metric. The 90% of user that don't reach the checkout page have a value of zero, but in practice they won't be in our experiment and won't contribute to the metric.
• Incorrectly estimate the variance in the total_purchases metric. The distribution of metric values is different if we include the 90% of users that have 0 purchases because they never reached the checkout page.

Thus, in cases when the experiment only includes a biased subset of users, it's possible the MDE and duration obtained by the power analysis won't be a good estimate.

One way to address this is to use data from a past experiment to estimate the power of a new, similar experiment (coming soon!). In our example, if we had a prior experiment that was also targeting the checkout page, we could use it to get better estimates of traffic volumes and metrics for this part of the product.

Inputs by Population Type

This is how the various inputs for the power analysis are obtained from the different population types:

Population	Mean and Variance Calculation	Total Exposures by Week Estimate
Everyone	Mean and variance across all users, estimated for 1, 2, 3, and 4 week rollups	Total count of users seen in the past 1, 2, 3, and 4 weeks
Targeting Gate	Mean and variance for users that pass the targeting gate, computed for 1, 2, 3, 4 week rollups	Total users that passed the targeting gate after 1, 2, 3, 4 weeks
Past Experiment	Cumulative mean and variance for the control group at 1, 2, 3, and 4 weeks	Total experiment exposures after 1, 2, 3, and 4 weeks, adjusted according to the past experiment's allocation and the desired allocation for the new experiment.
Qualifying Event	Mean and variance for users who logged a specified event, computed for 1, 2, 3, 4 week rollups	Total users who logged a specified event after 1, 2, 3, 4 weeks

Analysis Types

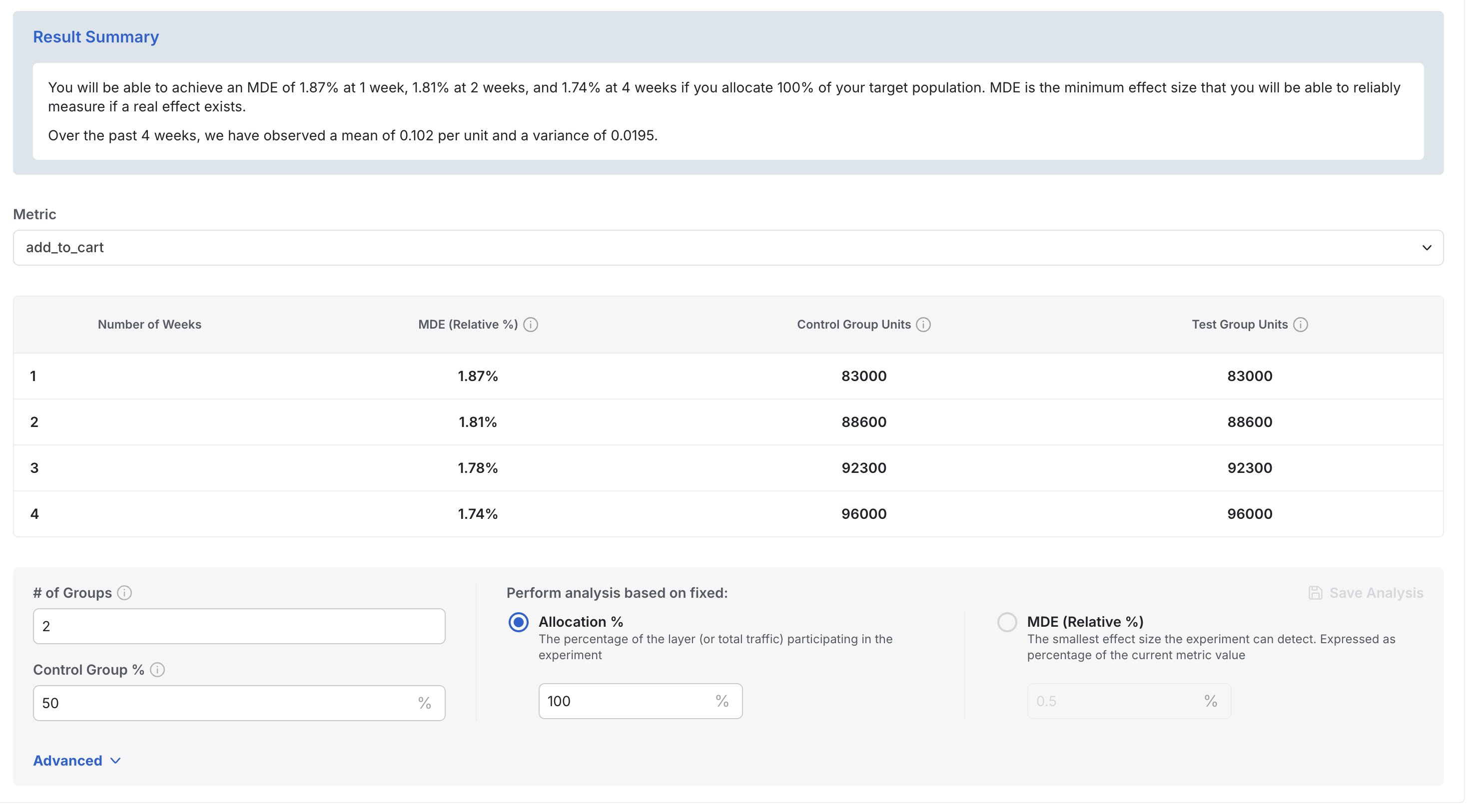
Fixed Allocation Analysis

Choose this option to understand how the length of the experiment impacts the MDE. The example below shows how the MDE for a page load metric shrinks over time in an experiment with 100% allocation. After 1 week we expect 5200 users per group and an MDE of 21.6%, by week 4 the number of users per group should increase to ~48k and the MDE is reduced to 7%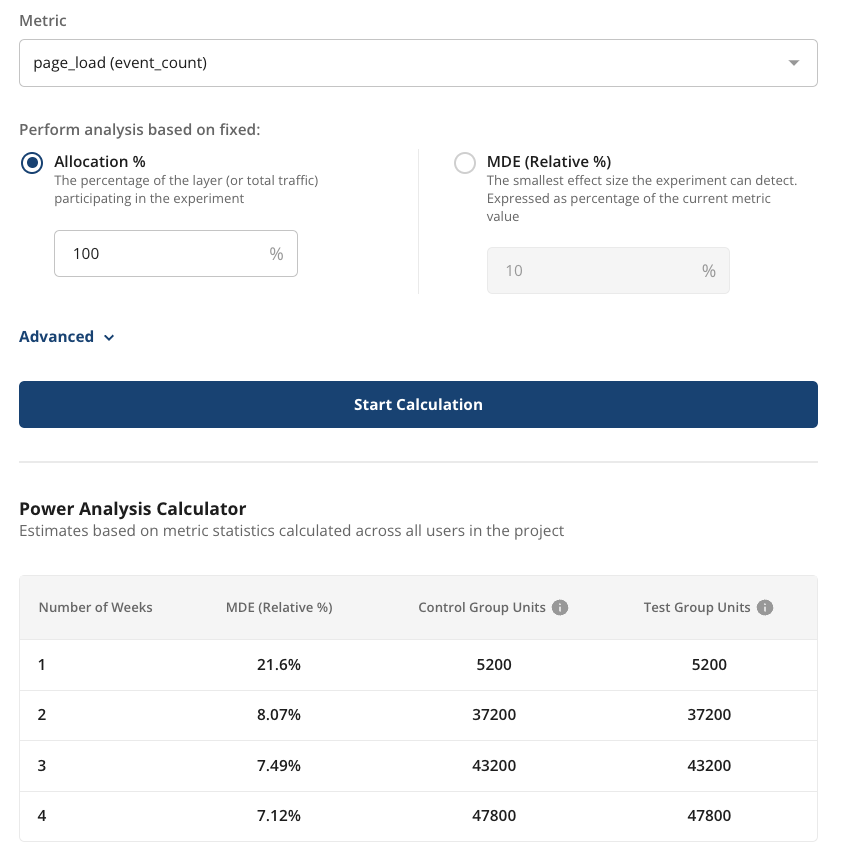

Fixed MDE Analysis

Choose this option if the smallest effect size that the experiment should detect is known. Enter the desired MDE as a percentage of the current metric value. For example: If a website currently gets 1,000 page loads per day, an MDE of 10% means we can detect a change of 100 or more page loads per day.

The results show the minimum number of weeks needed to reach this MDE for different allocation percentages. In the example below, the experiment should run for at least 2 weeks with 65% allocation or 4 weeks with 50% allocation. There's no way achieve the desired MDE in 1 week, as this would require more than 100% allocation (more users than we expect to see in one week).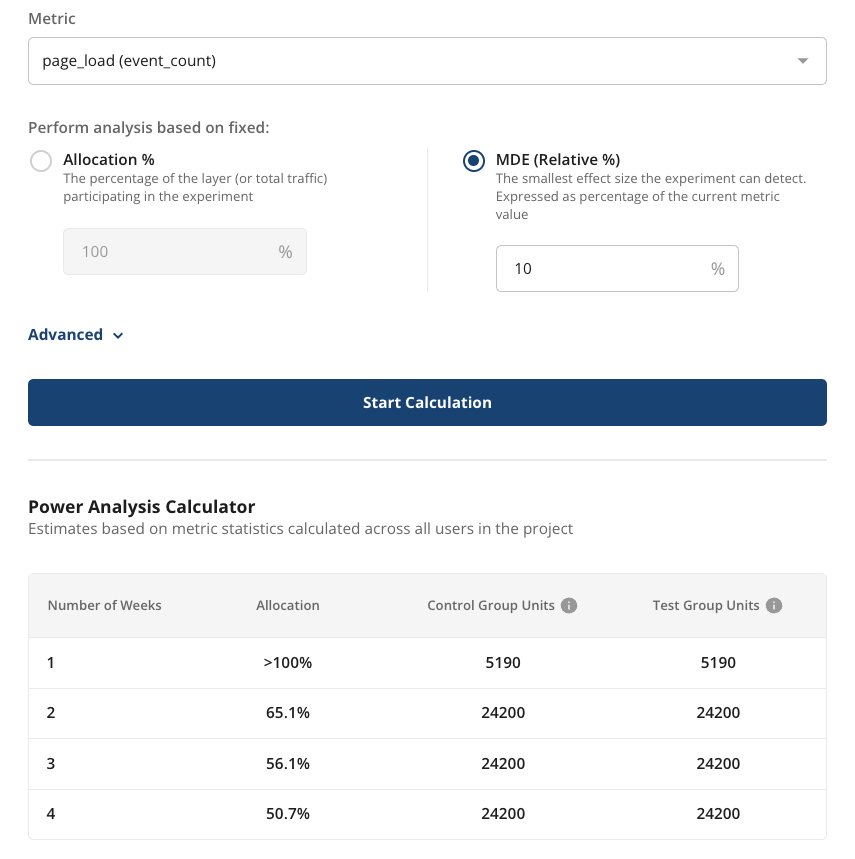

Advanced Options

Advanced settings to customize the analysis:

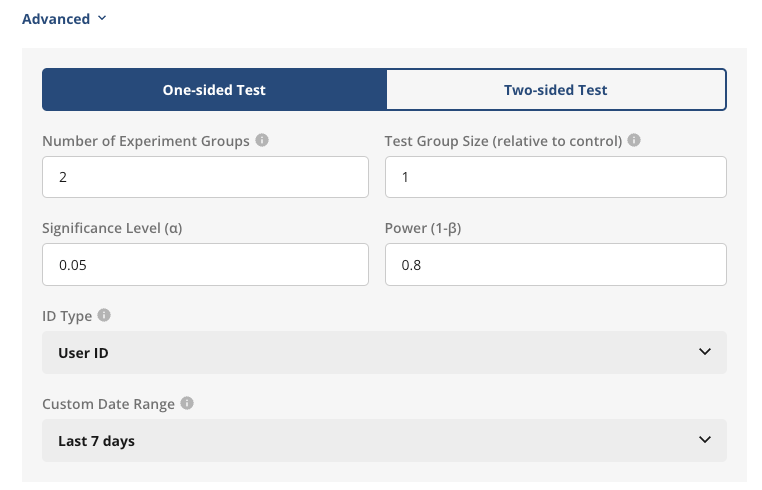
• Number of Experiment Groups: The total number of groups in the experiment, including control.
• Control Group %: What percent of users will be in the control group, e.g. 50% if half of all users will be control.
• Fixed Allocation or Fixed MDE Analysis: Different types of analyses you want to run. See here for more details.
• One-sided or Two-sided test: Toggle this setting to select the type of z-test to use for the analysis.
• Significant Level (α)
• Power (1-β)
• Bonferroni Correction Per Variant: Whether to include α correction for multiple tests in power analysis.

Calculation Details

The relative percentage MDE for a given metric X is computed using the following equation: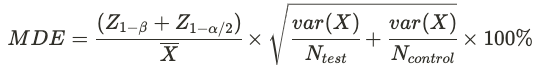

• X-bar is the mean metric value across all users
• var(X) is the population variance of the metric
• N_test and N_control are the estimated number of users in the test and control group. These are based on historical active user data along with experiment allocation and group size.
• Z_1-β is the standard Z-score for the selected power. Typically 1-β = 0.8 and Z_1-β = 0.84
• Z_1-α/2 is the standard Z-score for the selected significance level in a 2-sided test. Typically α = 0.05 and Z_1-α/2 = 1.96

Note: This calculation relies on statistics computed across the entire user base of the project. It does not account for the fact that experiments targeting only a subset of users may have different summary statistics for their key metrics. For example, the metric mean and variance can be different in an experiment that targets only Android users or one that exposes users at the lower part of an acquisition funnel.